Question

Show that the substitution u = y' leads to a bernoulli equation. solve this equation (see section 2.5). xy'' = y' + (y' )3

Answer 1

`xy''=y'+(y')^3`

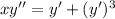
If
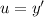
`u=y'`, then
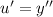
`u'=y''` and we have


`xu'=u+u^3`

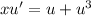
Divide both sides by
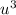
`u^3`, so that we get


`xu^(-3)u'=u^(-2)+1`

This is the Bernoulli equation we wanted to find. So we can substitute
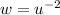
`w=u^(-2)`. This gives
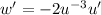
`w'=-2u^(-3)u'`, so the ODE is equivalent to


`-\frac12xw'=w+1`

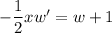
which is linear in
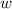
`w`. Multiply both sides by
`x` and rearrange terms a bit to get



`\frac12xw'+w=-1\implies x^2w'+2xw=-2x`

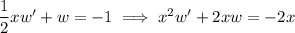
and now the LHS contains a derivative of a product, namely


`(x^2w)'=-2x\implies x^2w=-x^2+C\implies w=Cx^(-2)-1`

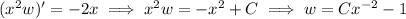
Now you can solve for
`u`, then integrate that result to find
`y`.