Question

PLEASE HELP which of the following identities? Check all that apply

Answer 1

`\sin(x - \pi) = \sin(x) \cos(\pi) - sin(\pi) \cos(x)`
via the angle sum formula of sin

`since \: cos(\pi) = - 1 \: and \: sin(\pi) = 0 \: then \\ sin(x - \pi) = - sin(x) \: which \: proves \: the \: first \: choice`


`\cos(x + y) + cos(x - y) = 2 \cos(x) \cos(y) =\:cos(x + y) + cos(x - y)=cos(x) cos(y)-sin(x)sin(y) +cos(x)cos(y)+sin(x)sin(y)=2cos(x)cos(y)`
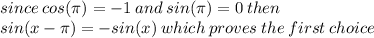
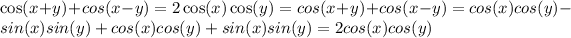
which proves the second choice
the third choice is wrong since for x=0,y=0 it will show that 2=1 which is incorrect
for the fourth one you can do some thing similar to choice one just expand the sum formula of sin and that should be true too
so
the first , the second and the fourth are all true

Answer 2

The identities which are true are:

A)

`\sin (x-\pi)=-\sin x`

B)

`\cos (x+y)+\cos (x-y)=2\cos x\cos y`

D)

`\sin (x+y)-\sin (x-y)=2\cos x\sin y`

Explanation:

A)

`\sin (x-\pi)=-\sin x`

We know that:

`\sin (x-\pi)=\sin (-(\pi-x))\\\\i.e.\\\\\sin (x-\pi)=-\sin (\pi-x)`

( since we know that:

`\sin (-x)=-\sin x` )

Also,

`\sin (\pi-x)=\sin x`

Hence, we get:

`\sin (x-\pi)=-\sin x`

This identity is true.

B)

`\cos (x+y)+\cos (x-y)=2\cos x\cos y`

We know that:

`\cos (x+y)=\cos x\cos y-\sin x\sin y`

and

`\cos (x-y)=\cos x\cos y+\sin x\sin y`

Hence, we get:

`\cos (x+y)+\cos (x-y)=\cos x\cos y-\sin x\sin y+\cos x\cos y+\sin x\sin y\\\\i.e.\\\\\cos (x+y)+\cos (x-y)=2\cos x\cos y`

Hence, this identity is true.

C)

`\cos (x+y)+\cos (x-y)=\cos^2x-\sin^2y`

Let us take x=0 and y=0 then we have:

`\cos (0)+\cos (0)=\cos^20-\sin^20\\\\i.e.\\\\1+1=1-0\\\\i.e.\\\\2=1`

which can't be possible.

Hence, this identity is not true.

D)

`\sin (x+y)-\sin (x-y)=2\cos x\sin y`

We know that:

`\sin (x+y)=\sin x\cos y+\cos x\sin y`

and

`\sin (x-y)=\sin x\cos y-\cos x\sin y`

Hence, we get:

`\sin (x+y)-\sin (x-y)=\sin x\cos y+\cos x\sin y-(\sin x\cos y-\cos x\sin y)`

i.e.

`\sin (x+y)-\sin (x-y)=\sin x\cos y+\cos x\sin y-\sin x\cos y+\cos x\sin y`

i.e.

`\sin (x+y)-\sin (x-y)=2\cos x\sin y`

Hence, this identity is true.