Question

I'm really not sure about this question and could use some help. Thanks in advance!!

Tom has taken out a loan for college. He started paying off the loan with a first payment of $200. Each month he pays, he wants to pay back 1.2 times as the amount he paid the month before. Explain to Tom how to represent his first 30 payments in sigma notation. Then explain how to find the sum of his first 30 payments, using complete sentences. Explain why this series is convergent or divergent.

Answer 1

Tom started out paying $200, namely the first term in that "geometric sequence" is $200.

and the next payment will be 1.2 times more than the previous, so, if the previous one was 200, the next one will be 200*1.2, and the next after that (200*1.2) * 1.2 and so on.

in a geometric sequence, to get the next term, we simply use a "multiplier", namely the "common ratio", in this case that'd be 1.2.

sigma notation wise,


`\bf \qquad \qquad \textit{sum of a finite geometric sequence} \\\\ S_n=\sum\limits_(i=1)^(n)\ a_1\cdot r^(i-1)\implies S_n=a_1\left( \cfrac{1-r^n}{1-r} \right)\quad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ ----------\\ n=30\\ a_1=200\\ r=1.2 \end{cases} \\\\\\ \sum\limits_(i=1)^(30)~200(1.2)^(i-1)`

and its sum will just be


`\bf \qquad \qquad \textit{sum of a finite geometric sequence} \\\\ S_n=\sum\limits_(i=1)^(n)\ a_1\cdot r^(i-1)\implies S_n=a_1\left( \cfrac{1-r^n}{1-r} \right)\quad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ ----------\\ n=30\\ a_1=200\\ r=1.2 \end{cases}`


`\bf S_(30)=200\left( \cfrac{1-1.2^(30)}{1-1.2} \right)\implies S_(30)=200\left( \cfrac{1-\stackrel{\approx}{237.37631}}{-0.2} \right) \\\\\\ S_(30)=200\left(\cfrac{\stackrel{\approx}{-236.37631}}{-0.2} \right)\implies S_(30)=200(1186.88) \\\\\\ S_(30)\approx 237366.3137998`

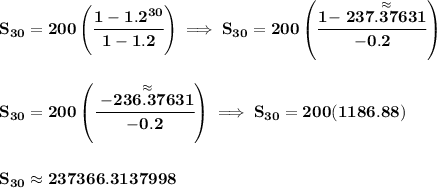
in plain and short, when the "common ratio" is a fraction, namely less than 1 and less than 0, the serie is convergent, namely it approaches a certain fixed amount.

in this case the common ratio is 1.2, and so is not 0 < | r | < 1, so the serie is divergent, namely it keeps on going.