Question

Question (c)! How do I know that t^5-10t^3+5t=0?
Thanks!

Answer 1

(a) By DeMoivre's theorem, we have


`(\cos\theta+i\sin\theta)^5=\cos5\theta+i\sin5\theta`

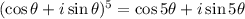
On the LHS, expanding yields


`\cos^5\theta+5i\cos^4\theta\sin\theta-10\cos^3\theta\sin^2\theta-10i\cos^2\theta\sin^3\theta+5\cos\theta\sin^4\theta+i\sin^4\theta`

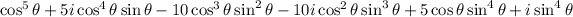
Matching up real and imaginary parts, we have for (i) and (ii),



`\cos5\theta=\cos^5\theta-10\cos^3\theta\sin^2\theta+5\cos\theta\sin^4\theta`

`\sin5\theta=5\cos^4\theta\sin\theta-10\cos^2\theta\sin^3\theta+\sin^5\theta`

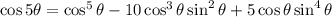
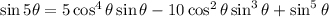
(b) By the definition of the tangent function,


`\tan5\theta=(\sin5\theta)/(\cos5\theta)`

`=(5\cos^4\theta\sin\theta-10\cos^2\theta\sin^3\theta+\sin^5\theta)/(\cos^5\theta-10\cos^3\theta\sin^2\theta+5\cos\theta\sin^4\theta)`


`=(5\tan\theta-10\tan^3\theta+\tan^5\theta)/(1-10\tan^2\theta+5\tan^4\theta)`

`=(t^5-10t^3+5t)/(5t^4-10t^2+1)`


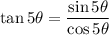
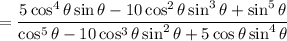
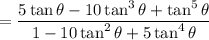
(c) Setting
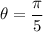
`\theta=\frac\pi5`, we have
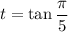
`t=\tan\frac\pi5` and
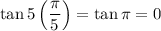
`\tan5\left(\frac\pi5\right)=\tan\pi=0`. So


`0=(t^5-10t^3+5t)/(5t^4-10t^2+1)`

At the given value of
`t`, the denominator is a non-zero number, so only the numerator can contribute to this reducing to 0.



`0=t^5-10t^3+5t\implies0=t^4-10t^2+5`

Remember, this is saying that


`0=\tan^4\frac\pi5-10\tan^2\frac\pi5+5`

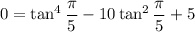
If we replace
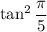
`\tan^2\frac\pi5` with a variable
`x`, then the above means
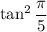
`\tan^2\frac\pi5` is a root to the quadratic equation,


`x^2-10x+5=0`

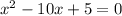
Also, if
`\theta=\frac{2\pi}5`, then
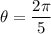
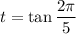
`t=\tan\frac{2\pi}5` and
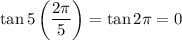
`\tan5\left(\frac{2\pi}5\right)=\tan2\pi=0`. So by a similar argument as above, we deduce that
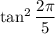
`\tan^2\frac{2\pi}5` is also a root to the quadratic equation above.

(d) We know both roots to the quadratic above. The fundamental theorem of algebra lets us write


`x^2-10x+5=\left(x-\tan^2\frac\pi5\right)\left(x-\tan^2\frac{2\pi}5\right)`

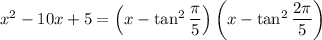
Expand the RHS and match up terms of the same power. In particular, the constant terms satisfy


`5=\tan^2\frac\pi5\tan^2\frac{2\pi}5\implies\tan\frac\pi5\tan\frac{2\pi}5=\pm\sqrt5`

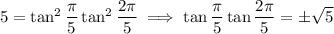
But
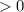
`\tanx>0` for all
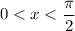
`0<x<\frac\pi2`, as is the case for
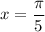
`x=\frac\pi5` and
`x=\frac{2\pi}5`, so we choose the positive root.