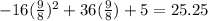Question

A ball is thrown into the air with an upward velocity of 36 ft/s. Its height h in feet after t seconds is given by the function h = −16t2 + 36t + 5. In how many seconds does the ball reach its maximum height? Round to the nearest hundredth if necessary. What is the ball’s maximum height?

Answer 1

To find the the maximum value of a function, we set the first derivative equal to 0 and solve for the critical points. The first derivative is:

h'(t) = -32t + 36

Now we will find the critical points:

-32t + 36 = 0

-4(8t-9) = 0

8t - 9 = 0

t = 9/8

As a decimal, the answer is 1.125

To find the maximum height, we plug t = 1.125 into h(t):

h(1.125) = -16(1.125)^2 + 36(1.125) + 5 = 25.25

So the maximum height is 25.25 feet at 1.13 seconds.

Answer 2

25.25 m

Explanation:

The path of the ball is modeled by a quadratic. Depending on which way it is facing, a quadratic
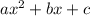`ax^(2) +bx+c` always has a either a minimum value or a maximum value. Always. Each quadratic can have either one or the other, never both. The first step in finding this minimum or maximum value is first finding the x value that gives out this minimum/maximum value when substituted into the function. There are many ways of doing this, one of them being:

x =
`(-b)/(2a)`

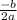
After finding this x, substitute this into the initial function and you have your minimum/maximum value.

So for this question h =
`-16t^(2)+36t+5`

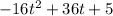
so t =
`(-36)/(2(-16))` =
`(9)/(8)`

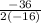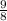
Again this is not the maximum value of the function but it is the input value that gives out the maximum height. We find this by plugging in the calculated t.

maximum height =
`-16((9)/(8) )^(2) +36((9)/(8) )+5=25.25`