Answer:
Explanation:
Given is a regular hexagon with apothem 3 square root 3 mm.
We have hexagon regular can be divided into 6 equilateral triangles with common vertex at the centre of the hexagon
Each equilateral triangle will have
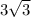 as apothem
as apothem
Hence using equilateral triangle property
we have side = a (say)
Then
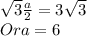
Area of each triangle = 1/2 bh = 9 sqrt 3
Hence area of hexagon =
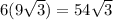
Use sqroot 3 = 1.732
we get
93.53 square mm.