check the picture below.
the blue inequality, overlaps the yellow one, on the right-hand-side, and where they overlap, is where the solution is, namely all those values or points.
now, is (-2,2) one of those values in that shaded area solution?
well, we can always check, is only true if that point resolves TRUE for the 1st inequality and TRUE also for the 2nd inequality, and that's how you get the shading btw, by checking their TRUE/FALSE values for each region, so let's check -2,2
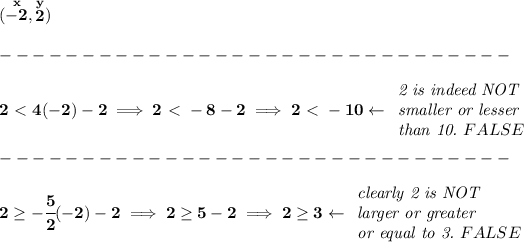
btw, we didn't have to check the 2nd inequality, once either one of them is FALSE, the whole solution itself is false for that point, but anyway, it ended false for both, so (-2, 2) is not in the solution area, and you can even see it in the graph, (-2, 2) is to the left-side of the red line, outside the shade.