Question

This system has one solution. {y=6x−11y=x2+4x−10 what is the y-coordinate of the solution?

Answer 1

i took the test and the answer was

-5

Answer 2

y-coordinate of the solution is, -5

Explanation:

Given the system of equations:

`y = 6x-11`

`y= x^2+4x-10`

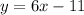
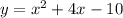
Equate these two equations we have;

`6x-11 = x^2+4x-10`

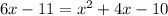
Subtract 6x from both sides we have;

`-11 = x^2-2x-10`

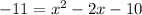
Add 11 both sides we have;

`0= x^2-2x+1`

Using the identity rule:

`(a-b)^2 = a^2-2ab+b^2`

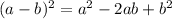
then;

`x^2-2x+1 = 0`

⇒
`(x-1)^2 = 0`

⇒
`x-1 = 0`

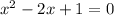
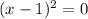
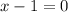
⇒x = 1

Substitute the value of x in
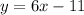`y = 6x-11` we have;

`y = 6(1)-11 = 6-11 = -5`

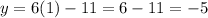
therefore, the y-coordinate of the solution is, -5