Answer:
Option: A is the correct answer.
A)

Explanation:
We know that a geometric series of the type:
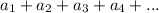
where
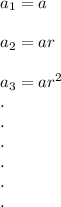
converges if r<1
Hence, we will check in each of the given options for which r<1
B)

From this series we observe that the common ratio i.e. r=2
Since,
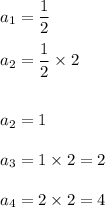
and so on.
Hence, the series is not convergent.
Hence, option: B is incorrect.
C)

From this series we observe that the common ratio i.e. r=3>1
Hence, the series diverges.
Hence, option: C is false.
D)
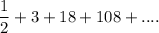
In this geometric series trhe common ratio is: 6>1
Hence, the series does not converge.
Hence, option D is incorrect.
A)

Here we have:
common ratio i.e. r=1/2<1
Hence, the geometric series converge and the sum is given by:
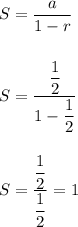
Hence, option: A is correct.