Answer:
C
Explanation:
We are given that a function
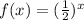
It can be write as
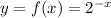
Taking log on both sides
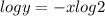
Differentiate w.r.t x
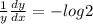
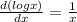
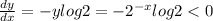 for all x
for all x
When f'(x) <0 then function is decreasing.
Hence, given function is decreasing function.
Substitute x=0 then we get
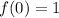 Because (
Because (
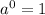 )
)
Therefore, y intercept is (0,1).
Domain pf function f(x)=R
Range of given function :(
 )
)
Hence, option C is true.