We're given the following function:
![f(x)=log(.75^x)=log[ ((3)/(4)) ^(x)]=log( (3^x)/(4^x))](https://img.qammunity.org/2019/formulas/mathematics/college/faa4xr469s5dy321fxxqg1tgmllp8pyd2m.png)
In order to see if the function is decreasing we'll take its derivative. If
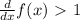
the function is increasing, if

the function is decreasing.
We take the derivate:
![(d)/(dx)[log( (3^x)/(4^x))]= (4^x)/(3^x)[ (d)/(dx) ((3^x)/(4^x))]=(4^x)/(3^x) (4^x[ (d)/(dx) (3^x)]-3^x[ (d)/(dx) (4^x)])/( 4^2^x)=](https://img.qammunity.org/2019/formulas/mathematics/college/pq69rhixqz31xxcpq93g3gj6utg6ymf0zk.png)
![(4^x)/(3^x) (4^x[3^xlog(3)]-3^x[4^x[4^xlog(4)])/( 4^2^x)=log(3)-log(4)\ \textless \ 0](https://img.qammunity.org/2019/formulas/mathematics/college/uk3hqj70alg15xioplnwgpkn0jush4mw6r.png) Which implies the function is decreasing.
Which implies the function is decreasing.
Another way to answer the problem (although less insightful) you can take any two real numbers

and
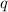
such that
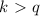
, then if
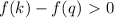
the function is increasing and if
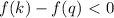
the function is decreasing. You can verify the function is decreasing with any two numbers in the function's domain.