Question

If (7, -4) is on the graph of F(x), which point must be on the graph of the inverse function F -1(x)?

Answer 1

Answer: The required point is (-4, 7).

Step-by-step explanation: Given that the point (7, -4) lies on the graph of the function
`f(x).`

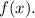
We are given to find a point that must lie on the graph of the inverse function
`f^(-1)(x).`

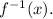
We know that

If a point (a, b) lies on the graph of a function
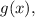`g(x),` then the point (b, a) must lie on the graph of the function
`g^(-1)(x).`

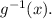
So, from the given information, we get

the point (-4, 7) must lie on the graph of the inverse function
`f^(-1)(x).`

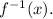
Thus, the required point is (-4, 7).

Answer 2

If (7, -4) is on the graph of F(x), then (-4, 7) is on the graph of F⁻¹(x).