Answer:
The equation of hyperbola with vertices at (0,±6) and asypmtotes at
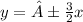
Explanation:
Given
vertices of hyperbola at (0,±6)
It means hyperbola along y axis and centre at (0,0)
Asymptotes
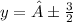
We know that equation of hyperbola along y axis
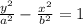
a=6
We know that the general equation of hyperbola asymptotes and vertcal transverse axis
y=
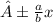
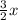 =
=
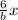
Both side cancel x we get
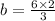
b=4
When we take
![-(3)/(2) =-\frac{6[tex]</p><p>b=(-6* (-2))/(3)]() }{b}x[/tex]
}{b}x[/tex]
Then we get b=4
Now, put the value of a and b in the equation of hyperbola we get
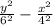 =1
=1
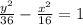
Hence, the required standard equation of hyperbola
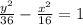 .
.