First we have to find the slope of the given line. We do that by puttiing the equation into slope-interept form. or solving it for y (same thing). 2x + 4y = -6. We move the 2x over by subtraction to get 4y = -2x - 6. Divide both sides by 4 to get the slope-intercept form we are seeking.
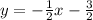. The slope that is perpendicular to that slope of -1/2 is the opposite reciprocal. Therefore, the perpendicular slope is a positive 2/1 or just 2. If this new line goes through the point (2, 5), it goes through the x value of 2 and the y value of 5. We will use those values along with the slope of 2 to solve for b in our slope-intercept equation. That looks like this:
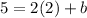and b = 1. That means our new equation, the one that is perpendicular to the given line, has an equation of y = 2x + 1.