Answer:
Domain:
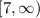
Range:
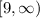
Explanation:
We have been given a function
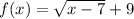 . We are asked to find the domain and range of our given function.
. We are asked to find the domain and range of our given function.
We know that a square root function is not defined for negative numbers, so domain of our given function would be
 .
.
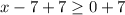

Therefore, the domain of our given function is all values of x greater than or equal to 7 that is
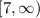 .
.
We know that range of a radical function of form
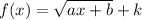 is
is
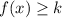 .
.
Upon looking at our given function, we can see that value of k is 9, therefore, the range of our given function is all values of y greater than or equal to 9 that is
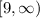 .
.