Answer:
Options A and D.
Explanation:
It is given in the question
Side AC = 6.9 cm
side BC = 9.8 cm
side AB = 12 cm
Let ∠BAC = x
We can find this angle x by applying sine and cosine rule in the given right angle triangle ABC
sinx =

=
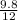
![x = sin^(-1)[(9.8)/(12)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/c98ii0knv014aovmmivndd9r7l4wthjjdc.png)
Now we apply cosine rule
cosx =
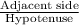
=
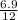
x =
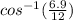
Therefore, options A and D are the correct options.