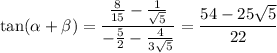Question

Tan α = - 4/3 lies in quad 2, and cos β = 2/3 lies in quad 1 find

a. cos(α + β)
b. sin( α+β)
c. t...

Answer 1

Recall some identities:



`\cos^2x+\sin^2x=1`


`\tan^2x+1=\sec^2x=\frac1{\cos^2x}`



`\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta`



`\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta`

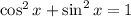
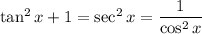
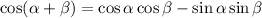
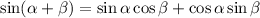
Not sure what part (c) is asking for, but I assume it's
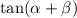
`\tan(\alpha+\beta)`, in which case



`\tan(\alpha+\beta)=(\sin(\alpha+\beta))/(\cos(\alpha+\beta))`


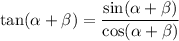
If
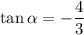
`\tan\alpha=-\frac43`, then


`\frac1{\cos^2\alpha}=1+\left(-\frac43\right)^2=\frac{25}9`

`\implies\cos\alpha=\pm\frac35`

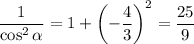
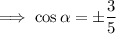
We know that
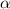
`\alpha` lies in quadrant 2, i.e.
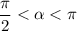
`\frac\pi2<\alpha<\pi`, so we expect
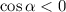
`\cos\alpha<0`. So we take the negative root. We also find that


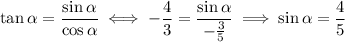
`\tan\alpha=(\sin\alpha)/(\cos\alpha)\iff-\frac43=(\sin\alpha)/(-\frac35)\implies\sin\alpha=\frac45`

If
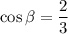
`\cos\beta=\frac23`, then



`\sin^2\beta=1-\left(\frac23\right)^2=\frac59\implies\sin\beta=\pm\frac{\sqrt5}3`


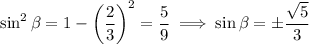
Since
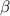
`\beta` lies in quadrant 1, i.e.
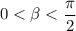
`0<\beta<\frac\pi2`, we know that
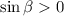
`\sin\beta>0`, so we take the positive root.


Now,


`\cos(\alpha+\beta)=-\frac35\cdot\frac23-\frac45\cdot\frac{\sqrt5}3=-\frac52-\frac4{3\sqrt5}`



`\sin(\alpha+\beta)=\frac45\cdot\frac23+\left(-\frac35\right)\cdot\frac{\sqrt5}3=\frac8{15}-\frac1{\sqrt5}`

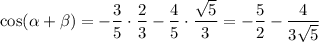
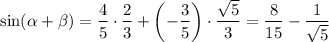
Then it follows that



`\tan(\alpha+\beta)=\frac{\frac8{15}-\frac1{\sqrt5}}{-\frac52-\frac4{3\sqrt5}}=(54-25\sqrt5)/(22)`