I added a screenshot with the complete question.
Answer:The radius increased by 0.6 in
Step-by-step explanation:1- getting the radius before the ball is fully inflated:volume of sphere =
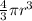
We are given that the volume before the ball is fully inflated is 180 in³. Therefore, we can solve for the radius as follows:
180 =
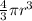
135 = π * r³
42.9718 = r³
radius = 3.5026 in
2- getting the radius after the ball is fully inflated:volume of sphere =
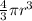
We are given that the volume after the ball is fully inflated is 294 in³. Therefore, we can solve for the radius as follows:
294 =
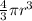
220.5 = π * r³
70.187 = r³
radius = 4.124958 in
3- getting the increase in the radius:increase in radius = radius after inflation - radius before inflation
increase in radius = 4.124958 - 3.5026
increase in radius = 0.622 which is approximately 0.6 in
Hope this helps :)