Answer:
Option A.
Explanation:
Remainder theorem: If a polynomial P(x) divided by (x-c), then the remainder is P(c). It means if c is a root of P(x), then P(c)=0.
The given polynomial is
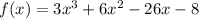
Substitute x=-4 in the given polynomial.

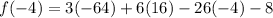
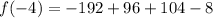
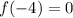
Similarly,
Substitute x=-2 in the given polynomial.
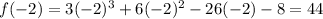
Substitute x=2 in the given polynomial.

Substitute x=4 in the given polynomial.
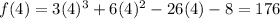
From the given options only at x=-4 the value of function is 0. It means remainder is 0 at x=-4.
-4 is a root of the given polynomial. Therefore the correct option is A.