Question

Use the remainder theorem to determine which number is a root of f(x) = 3x3 + 6x2 - 26x - 8. A) -4 B) -2 C) 2 D) 4

Answer 1

Option A.

Explanation:

Remainder theorem: If a polynomial P(x) divided by (x-c), then the remainder is P(c). It means if c is a root of P(x), then P(c)=0.

The given polynomial is

`f(x)=3x^3+6x^2-26x-8`

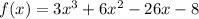
Substitute x=-4 in the given polynomial.

`f(-4)=3(-4)^3+6(-4)^2-26(-4)-8`

`f(-4)=3(-64)+6(16)-26(-4)-8`

`f(-4)=-192+96+104-8`

`f(-4)=0`

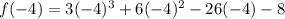
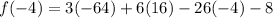
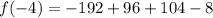
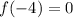
Similarly,

Substitute x=-2 in the given polynomial.

`f(-2)=3(-2)^3+6(-2)^2-26(-2)-8=44`

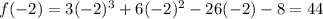
Substitute x=2 in the given polynomial.

`f(2)=3(2)^3+6(2)^2-26(2)-8=-12`

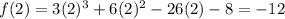
Substitute x=4 in the given polynomial.

`f(4)=3(4)^3+6(4)^2-26(4)-8=176`

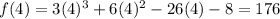
From the given options only at x=-4 the value of function is 0. It means remainder is 0 at x=-4.

-4 is a root of the given polynomial. Therefore the correct option is A.

Answer 2

Given that the function is given by:
f(x)=3x^3+6x^2-26x-8
To determine which number is a root we substitute the value in the equation, the value of x that we result in the function being a zero is the root of the equation.
First plugging in x=-4 in the expression gives us:
f(-4)=3(-4)^3+6(-4)^2-26(-4)-8
f(-4)=3(-64)+6(16)+104-8
simplifying the above we get:
f(-4)=0
This implies that x=-4 is a root of the function
thus the answer is:
A] -4