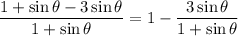Simplify this equation please. ( \csc^(2) ( \theta) - 3 \csc( \theta) + 2 )/( \csc^(2) ( \theta) - 1)

Question

Simplify this equation please.


`( \csc^(2) ( \theta) - 3 \csc( \theta) + 2 )/( \csc^(2) ( \theta) - 1)`

Answer 1

`(\csc^2\theta-3\csc\theta+2)/(\csc^2\theta-1)`

Identity:


`\sin^2\theta+\cos^2\theta=1\implies1+\cot^2\theta=\csc^2\theta`

So we can rewrite the denominator to get


`(\csc^2\theta-3\csc\theta+2)/(\cot^2\theta)`

Multiply numerator and denominator by
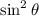
`\sin^2\theta`. Several terms will cancel since
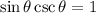
`\sin\theta\csc\theta=1`. Also,
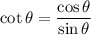
`\cot\theta=(\cos\theta)/(\sin\theta)`. We get


`(1-3\sin\theta+2\sin^2\theta)/(\cos^2\theta)`

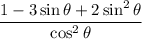
Factorize the numerator, and write
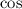
`\cos` in terms of
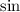
`\sin` in the denominator to factorize it further to get


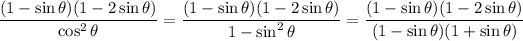
`((1-\sin\theta)(1-2\sin\theta))/(\cos^2\theta)=((1-\sin\theta)(1-2\sin\theta))/(1-\sin^2\theta)=((1-\sin\theta)(1-2\sin\theta))/((1-\sin\theta)(1+\sin\theta))`


The
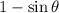
`1-\sin\theta` factors cancel, leaving you with


`(1-2\sin\theta)/(1+\sin\theta)`

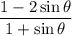
which you could simplify a bit further by writing


`(1+\sin\theta-3\sin\theta)/(1+\sin\theta)=1-(3\sin\theta)/(1+\sin\theta)`