A trinomial is given by the following formula:
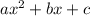
Identify a, b, and c in this trinomial:
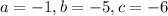
We'll pretend that all the numbers are positive.
Find all the factors of c:
Factors of 6: {1,2,3,6}
The numbers that multiply to 6 must also add up to b.
1 + 6 = 7
2 + 3 = 5
2 and 3 add up to 5. These numbers will be used for factoring:
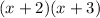
Because all of the numbers are negative, we have to add a negative sign in front of our factors:
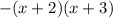
To find the other x-intercept, one of the values must be set to 0.

Subtract both sides by 2.

The other x-intercept for this trinomial is
x = -2.