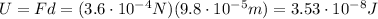The electric potential energy of the charge is equal to the potential at the location of the charge, V, times the charge, q:
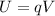
The potential is given by the magnitude of the electric field, E, times the distance, d:
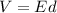
So we have
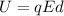
(1)
However, the electric field is equal to the electrical force F divided by the charge q:
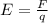
Therefore (1) becomes
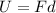
And if we use the data of the problem, we can calculate the electrical potential energy of the charge: