General Idea:
When t represents the time, h(t) represent the height of ball in meters after t seconds and you have an function of the form
 , and if
, and if
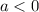 , then this function will reach maximum height at
, then this function will reach maximum height at
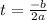 .
.
Since time cannot be positive,
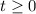 .
.
When ball is above the ground,
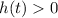 .
.
When the ball hit the ground
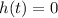
Applying the concept:
Setting up the function equal to zero to find the time it takes for the ball hit the ground.

Conclusion:
The Ball will be above the ground during the time interval
 .
.