Question

Anna throws a ball in the air from her balcony. The following equation models the height of the ball, in meters, after t seconds.

h(t)=5t^2+9t+80

Anna wants to rewrite the equation to determine after how many seconds the ball hits the ground. Use this situation to complete the following statements.

The function ...................reveals that the ball's .............above the ground will be .................meters after ..........seconds.

Answer 1

The function h(t) = -5(t + 3.2)(t - 5) reveals that the ball's height above the ground will be 0 meters after 5 seconds.

Answer 2

General Idea:

When t represents the time, h(t) represent the height of ball in meters after t seconds and you have an function of the form
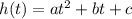`h(t) = at^2 + bt + c`, and if
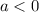`a < 0`, then this function will reach maximum height at
`t=(-b)/(2a)`.

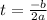Since time cannot be positive,
`t\geq 0`.

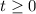When ball is above the ground,
`h(t)>0`.

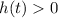When the ball hit the ground
`h(t) =0`

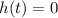
Applying the concept:

Setting up the function equal to zero to find the time it takes for the ball hit the ground.

`-5t^2+9t+80 =0\\ \\ Here\; a=-5; \; b=9; \; c = 80\\ \\ Using\; Quadratic \; formula \;\\ \\ t=(-b\pm √(b^2-4ac))/(2a) \\ \\ t=(-9\pm √(81-4(-5)(80)))/(2(-5)) \\ \\ t=(-9\pm √(81+1600))/(-10)\\ \\ t=(-9+41)/(-10) (or)t=(-9-41)/(-10)\\ \\ Since \; t \; cannot \; be \; negative\\ \\ t=(-50)/(-10)=5 \; seconds`

Conclusion:

The Ball will be above the ground during the time interval
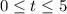`0\leq t\leq 5`.