Question

A 40-meter-long blade of a wind turbine makes one complete revolution in 10 seconds. To the nearest tenth, the linear velocity of the blade is ____meters per second.

Answer 1

The answer is 25.1 m/s

Explanation:

In order to determine the linear velocity of the blade, we have to know about circles.

In any circle, the expression of its perimeter is:

`P=2\pi R`

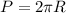
Where:

P=Perimeter of the circle

R=Radius of the circle.

To determine the linear velocity, first we have to determine the perimeter that the long blade describes.

The long blade lengths 40 meters. This value represents the radius of the circle movement. Then the perimeter is:

`R=40\\P=2\pi (40)\\P=80\pi`

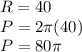
Then, the linear velocity is the rate of the perimeter per one complete revolution:

`V=(P)/(T)=(80\pi )/(10)=8*3.142=25.136`

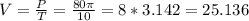
We have to round the final value to the nearest tenth. I have attached an image that shows the position of the nearest tenth.

Finally, the linear velocity is 25.1 m/s.

Answer 2

The distance the tip travels is
2π·(40 m) = 80π m

Then its speed is
(80π m)/(10 s) = 8π m/2 ≈ 25.1 m/s