Answer: There is a difference of $ 1.0228.
Explanation: Given, initial amount or principal = $ 1000,
Time= 5 years and given compound rate of interest = $3.7%
Now, Since the amount in compound continuously,
 , where, r is the rate of compound interest, P is the principal amount and t is the time.
, where, r is the rate of compound interest, P is the principal amount and t is the time.
Here, P=$ 1000, t=5 years and r= $3.7%,
Thus, amount in compound continuously ,
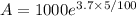
⇒
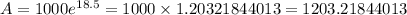
Therefore, interest in this compound continuously rate =1203.21844013-1000=203.21844013
now, Since the amount in compound quarterly,
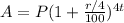 , where, r is the rate of compound interest, P is the principal amount and t is the time.
, where, r is the rate of compound interest, P is the principal amount and t is the time.
Thus, amount in compound quarterly,
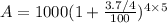
⇒

⇒

⇒
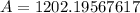
Therefore, interest in this compound quarterly rate=1202.19567617-1000=202.19567617
So, the difference in these interests=203.21844013-202.19567617=1.02276396 ≈1.0228