Answer:
The piece of wire cut for the square is 180.3 inches, and the piece of wire cut for the circle is 159.7 inches.
----------------
Step-by-step explanation:
Use the following formulas for the areas of a square and circle:
Square
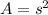
Circle
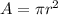
s represents the length of the side in a square, and r represents the radius of the circle.
Set these two equations to be equal to each other.
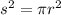
We can simplify this by square rooting both sides to get s by itself:
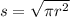
Now we'll find the perimeter of the square and the circumference of the circle. Use the following formulas for the perimeter and circumference:
Square
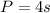
Circle
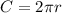
The perimeter and circumference must both equal 340, so set the equations to add together to become 340:
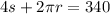
Because we know what s equals, we can plug it into this equation:
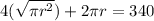
Simplify the equation by dividing both sides by 2 and extracting r from the first term.

Assuming pi = 3.1416, replace pi with this decimal value and solve:
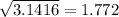

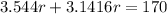

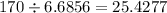
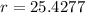
Rounded to the nearest tenth, the radius of the circle is 25.4.
We can now use the radius to find the circumference of the circle:

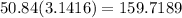
Rounded to the nearest tenth, the circumference of the circle is
159.7 inches.Plug this value into the original equation for the perimeter and circumference:
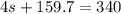
Subtract 159.7 from both sides.
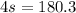
The perimeter of the square is
180.3 inches.