Question

PLEASE HELP!!!!! A wire 340 in. long is cut into two pieces. One piece is formed into a square and the other into a circle. If the two figures have the same area, what are the lengths of the two pieces of wire (to the nearest tenth of an inch)?

Answer 1

Answer:
The piece of wire cut for the square is 180.3 inches, and the piece of wire cut for the circle is 159.7 inches.
----------------
Step-by-step explanation:
Use the following formulas for the areas of a square and circle:

Square

`A = s^(2)`

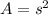
Circle

`A = \pi r^(2)`

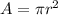
s represents the length of the side in a square, and r represents the radius of the circle.

Set these two equations to be equal to each other.


`s^(2) = \pi r^(2)`

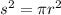
We can simplify this by square rooting both sides to get s by itself:


`s = \sqrt{\pi r^(2)}`

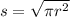
Now we'll find the perimeter of the square and the circumference of the circle. Use the following formulas for the perimeter and circumference:

Square

`P = 4s`

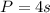
Circle

`C = 2 \pi r`

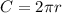
The perimeter and circumference must both equal 340, so set the equations to add together to become 340:


`4s + 2 \pi r = 340`

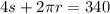
Because we know what s equals, we can plug it into this equation:


`4( \sqrt{\pi r^(2)} ) + 2 \pi r = 340`

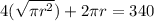
Simplify the equation by dividing both sides by 2 and extracting r from the first term.


`2r( √(\pi) ) + \pi r = 170`

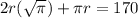
Assuming pi = 3.1416, replace pi with this decimal value and solve:


`√(3.1416) = 1.772`


`2r(1.772) + 3.1416r = 170`


`3.544r + 3.1416r = 170`


`6.6856r = 170`


`170 / 6.6856 = 25.4277`


`r = 25.4277`

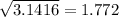
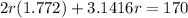
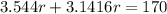
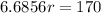
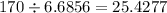
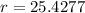
Rounded to the nearest tenth, the radius of the circle is 25.4.

We can now use the radius to find the circumference of the circle:


`2\pi(25.42)`


`50.84(3.1416) = 159.7189`

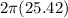
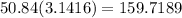
Rounded to the nearest tenth, the circumference of the circle is 159.7 inches.

Plug this value into the original equation for the perimeter and circumference:


`4s + 159.7 = 340`

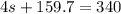
Subtract 159.7 from both sides.


`4s = 180.3`

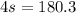
The perimeter of the square is 180.3 inches.