Question

Use the Quadratic Formula to solve the equation. -2x^2 - 5x + 5 = 0

Answer 1

The answer is going to be in the picture because trying to make fractions with this is too difficult. :D

Answer 2

`x = (5 \pm √( 65 ))/(-4)`.

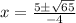Explanation:

The Quadratic Formula for a second degree polynomial
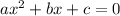`ax^(2) +bx+c=0` is a formula for the values of its solution i.e. for finding the values of x.

It is given by,
`x = \frac{-b \pm\sqrt{b^(2)-4ac }}{2a}`.

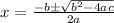Now, we have the given quadratic equation
`-2x^(2)-5x+5 = 0`,

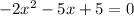which gives a = -2 , b = -5 , c = 5.

Substituting the value of a, b , c in the above formula, we get

`x = \frac{-(-5) \pm \sqrt{(-5)^(2) -4 * (-2) * 5 }}{2 * (-2)}`.

`x = (-(-5) \pm √( 25 + 40 ))/(-4)`.

`x = (5 \pm √( 65 ))/(-4)`.

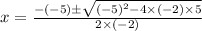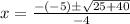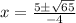Hence, the solution of the given quadratic equation is
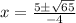`x = (5 \pm √( 65 ))/(-4)`.