Question

Secant BE and CF intersect at point A inside D. What is the measure of BF?

Answer 1

`\text{BF}=80^(\circ)`

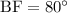
Explanation:

We have been given a circle D. Secant BE and CF intersect at point A inside D. We are asked to find the measure of arc BF.

We know that when two secants intersect inside a circle, then the measure of angle formed is half the sum of intercepting arcs.

`m\angle EAF=\frac{\text{Measure of arc EF+Measure of arc BC}}{2}`

`70^(\circ)=\frac{\text{Measure of arc EF+Measure of arc BC}}{2}`

`2*70^(\circ)=\frac{\text{Measure of arc EF+Measure of arc BC}}{2}*2`

`140^(\circ)=\text{Measure of arc EF+Measure of arc BC}`

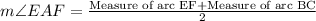
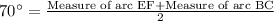
We know that degree measure of circumference of circle is 360 degrees, so we can set an equation as:

`\text{Arc EF+BC+EC+BF}=360^(\circ)`

`140^(\circ)+140^(\circ)+\text{BF}=360^(\circ)`

`280^(\circ)+\text{BF}=360^(\circ)`

`280^(\circ)-280^(\circ)+\text{BF}=360^(\circ)-280^(\circ)`

`\text{BF}=80^(\circ)`

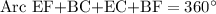
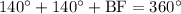
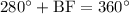
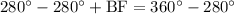
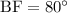
Therefore, the measure of arc BF is 80 degrees.