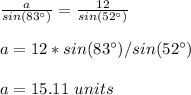Answer:
Part 1)
Part a)
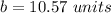
Part b)
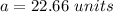 (three different ways in the procedure)
(three different ways in the procedure)
Part 2)
First triangle (triangle a)
Part a)

Part b)
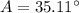
Part c)
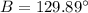
Second triangle (triangle b)
Part a)
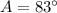
Part b)
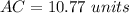
Part c)
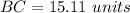
Explanation:
Part 1)
Part A
we know that
In the right triangle ABC

we have
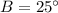
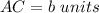
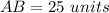
Substitute and solve for b
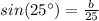

Part B
First way
we know that
In the right triangle ABC
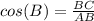
we have
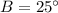
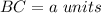
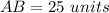
Substitute and solve for a
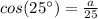
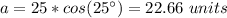
Second way
Applying the Pythagoras theorem
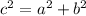
we have
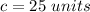
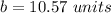
substitute and solve for a
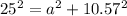
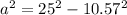

Third way
we know that
In the right triangle ABC
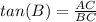
we have
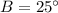
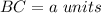

substitute and solve for a
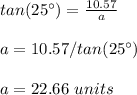
Part 2)
triangle a
we have
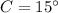

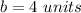
Step 1
Find the measure of length side c
Applying the law of cosines
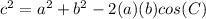
substitute
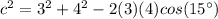
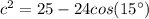

Step 2
Find the measure of angle A
Applying the law of sines

we have


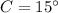
substitute and solve for A
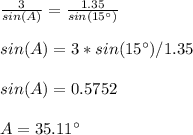
Step 3
Find the measure of angle B
Remember that the sum of the internal angles of a triangle must be equal to
 degrees
degrees
so
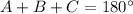
we have
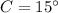
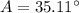
substitute
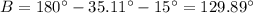
triangle b
we have
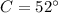

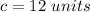
Step 1
Find the measure of angle A
Remember that the sum of the internal angles of a triangle must be equal to
 degrees
degrees
so
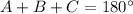
we have
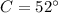

substitute
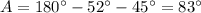
Step 2
Find the measure of side AC
Applying the law of sines
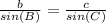
we have
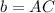
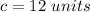

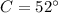
substitute and solve for b
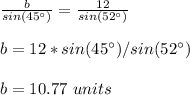
Step 3
Find the measure of side BC
Applying the law of sines

we have
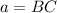
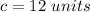
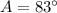
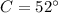
substitute and solve for a