Because the amount of radioactive sample left at time t, N(t), is related to the initial amount of the radioactive sample at time t=0 by the law
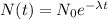
where
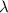
is the decay rate of the sample. If we are able to measure the fraction of sample left at time t,
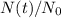
, we can estimate its age t, but only if we know the decay rate of the sample,
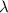
. Without knowing this value, we cannot estimate t from the equation.