Question

Which is the absolute value function corresponding to the graph with these characteristics?

•Vertex is at (-2, k)
•V-shaped graph •Opens in the downward direction
•Coefficient a is (+/-)4
•Left arm passes through point (-3, -1)


A. y = 4|x − 2|



B. y = 4|x − 2| + 3



C. y = -4|x + 2| + 3



D. y = -4|x + 2| − 3

Answer 1

the correct answer would be C

Answer 2

The parent function for an absolute value function is:


`y=a|x-h|+k`

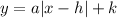
If a is positive, the graph will open upward, and if a is negative, it will open downward. Given that the graph opens downward, we know a must be negative.

Next, h represents the horizontal shift of the graph. Given that the vertex is at (-2,k), we know that h = 2.

The k value does not matter because in the given characteristics we are given a general k value that will work with any graph.

Finally, we need to find which graph passes through (-3, -1). To meet the requirements discussed above, we can narrow the answer to C or D. Now just plug in -3 for x in both functions, and whichever one equals -1 at x=-3 is our answer:

C) -4|-3 + 2| + 3 = -4(1) + 3 = -1

D) -4|-3 + 2| - 3 = -4(1) - 3 = -7

The answer is C.