Question

It takes 5.2 minutes for a 4.0 g sample of francium-210 to decay until only 1.0 g is left. What is the half-life of francium-210? 7.8 minutes 1.3 minutes 2.6 minutes 5.2 minutes

Answer 1

This problem is not about chemistry it is about math. the half-life of a certain thing is the time that it needs to decay 50% of what it had before. so if there is 4g, after 1 half there will be only 2g. so to become 1g it is passed 2 half-lives. 4,0g, 2,0g, 1,0g so it is the time divided by 2( numbers of half-lives). So the half-life of Francium 210 is 2,6 min.

Answer 2

Answer: The half life of the reaction is 2.6 minutes.

Step-by-step explanation:

Rate law expression for first order kinetics is given by the equation:

`k=(2.303)/(t)\log([A_o])/([A])`

where,

k = rate constant = ?

t = time taken for decay process = 5.2 minutes

`[A_o]` = initial amount of the reactant = 4.0 g

[A] = amount left after decay process = 1.0 g

Putting values in above equation, we get:

`k=(2.303)/(5.2min)\log(4.0)/(1.0)\\\\k=0.267min^(-1)`

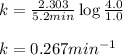
The equation used to calculate half life for first order kinetics:

`t_(1/2)=(0.693)/(k)`

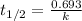
We are given:

`k=0.267min^(-1)`

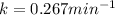
Putting values in above equation, we get:

`t_(1/2)=(0.693)/(0.267min^(-1))=2.6min`

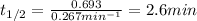
Hence, the half life of the reaction is 2.6 minutes.