Question

The table represents f(x), and the graph represents g(x). Which statements about the functions are true for the interval [4, 10]?

x     f(x)
3     1.33
4     1
5     0.8
6     0.66
10   0.4

A) The average rate of change of f(x) is greater than the average rate of change of g(x).
B) The average rate of change of f(x) is less than the average rate of change of g(x).
C) Both functions have the same average rate of change.
D) The average rate of change of f(x) is 0.1, and the average rate of change of g(x) is 0.25.
E) The average rate of change of f(x) is -0.1, and the average rate of change of g(x) is -0.25.

Answer 1

The statements which are true for the functions f(x) and g(x) are:

B) The average rate of change of f(x) is less than the average rate of change of g(x).

E) The average rate of change of f(x) is -0.1, and the average rate of change of g(x) is -0.25.

Explanation:

The average rate of change of a function is the ratio of the difference in x-value to the difference in y-value.

i.e. for a function f(x) the average rate of change of the function f(x) over the interval [a,b] is given by:

`Rate\ of\ change=(f(b)-f(a))/(b-a)`

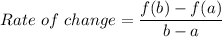
• The table of the function f(x) is given by:

x f(x)

3 1.33

4 1

5 0.8

6 0.66

10 0.4

Hence, the average rate of the function over [4,10] is:

`Rate\ of\ change=(f(10)-f(4))/(10-4)`

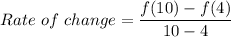
i.e.

`Rate\ of\ change=(0.4-1)/(10-4)`

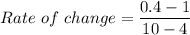
i.e.

`Rate\ of\ change=(-0.6)/(6)`

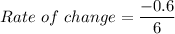
i.e.

`Rate\ of\ change=-0.1`

• By the graph of the function g(x) we observe that:

g(4)=2.5 and g(10)=1

Hence, the average rate of change of the function g(x) over the interval [4,10] is:

`Rate\ of\ change=(g(10)-g(4))/(10-4)`

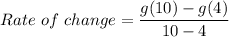
i.e.

`Rate\ of\ change=(1-2.5)/(10-4)`

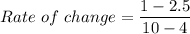
i.e.

`Rate\ of\ change=(-1.5)/(6)`

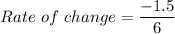
i.e.

`Rate\ of\ change=-0.25`

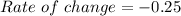
Since the modulus of the average rate of change for the function g(x) is greater than the function f(x)

Hence, g(x) has a greater average rate of change than f(x).

( Since, 2.5>0.1)

Answer 2

The rate of change for f(x) for the interval [4,10] will be approximated by:
=(Δ y-axis)/(Δ x-axis)
=(0.4-1)/(10-4)
=-0.1

Rate of change for g(x) for interval [4,10]
=(1-2.5)/(10-4)
=-0.25

from the above guesstimate we can deduce that average rate of change for f(x) is less than that of g(x). Thus the answer will be:
B) The average rate of change of f(x) is less than the average rate of change of g(x).