Question

Find one pair of real numbers, $(x,y),$ such that $x + y = 6$ and $x^3 + y^3 = 144.$

Answer 1

No real solution

Explanation:

Given that there are two real numbers x and y such that

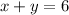`x+y =6` and
`x^3+y^3 =144`

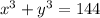
We can substitute for y as

`y=6-x`

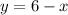
Substitute in II equation as

`(6-x)^3+x^3 =144\\216-108x+18x^2-x^3+x^3 =144\\x^2-6x+12=0`

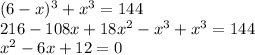
Solve this using quadratic formula

`x=(-6±√(36-48) )/(2) \\=-3±i√(3)`

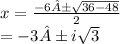
This shows that there cannot be any two real numbers satisfying the given condition

Answer 2

For this case we have the following system of equations:
x + y = 6
x ^ 3 + y ^ 3 = 144
Solving the system of equations graphically we have that one of the solutions is:
x = 3-root (5)
y = 3 + root (5)
Then, an ordered pair that satisfies both equations:
(x, y) = (3-root (5), 3 + root (5))
Answer:
(x, y) = (3-root (5), 3 + root (5))