Answer:
No real solution
Explanation:
Given that there are two real numbers x and y such that
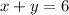 and
and
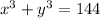
We can substitute for y as
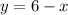
Substitute in II equation as

Solve this using quadratic formula
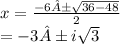
This shows that there cannot be any two real numbers satisfying the given condition