Question

What minimum speed must an electron have to excite the 492-nm-wavelength blue emission line in the hg spectrum?

Answer 1

The energy required by the excitation of the line is:
ΔE = hν = hc / λ
where:
ΔE = energy difference
h = Planck constant
ν = line frequency
c = speed of light
λ = line wavelength

The energy difference must be supplied by the electron, supposing it transfers all its kinetic energy to excite the line:

`\Delta E = (1)/(2) m v^(2)`

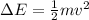
Therefore,

`(1)/(2) m v^(2) = (hc)/(\lambda)`

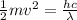
And solving for v we get:

`v = \sqrt{ (2hc)/(m\lambda) }`

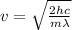
Plugging in numbers (after trasforing into the correct SI units of measurement):

`v = \sqrt{ ((2)(6.6 \cdot 10^(-34))(3 \cdot 10^(8)) )/((9.11 \cdot 10^(-31))(4.92 \cdot 10^(-7)) ) }`
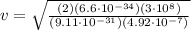
=9.4 · 10⁵ m/s

Hence, the electron must have a speed of 9.4 · 10⁵ m/s in order to excite the 492nm line.