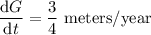a) Use the mean value theorem.

Since
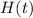
gives the tree's height in meters at time

, the value of
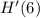
informs us how quickly the tree is growing exactly after 6 years have passed. (i.e. the instantaneous rate of change of the tree's height)
b) We use the mean value theorem again. Observe that

, and that
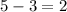
. By the MVT, there must be some
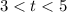
such that

c) The average height of the tree is given by the integral
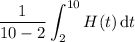
If you can remember the formula for the area of a trapezoid, then this is pretty easy to compute. With five data points, you end up with four trapezoids constructed by the four adjacent subintervals. The "bases" are given by the values of
at each pair of endpoints, and the "heights" are the lengths of the subintervals. For the integral itself, we get
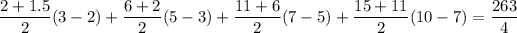
So the average height of the tree (in meters) is
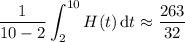
d) When
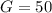
, the diameter of the base can be determined to be
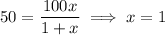
We're told that
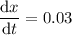
.
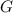
is a function of

which is in turn a function of

, so when we differentiate, we use the chain rule:
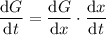

When the height of the tree is 50 meters, we found the diameter to be 1 meter, so at this point