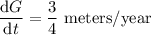Question

The height of a tree at time t is given by a twice-differentiable function H, where H(t) is measured in meters and t is measured in years. Selected values of H(t) are given in the table above.

(a) Use the data in the table to estimate H'(6). Using correct units. interpret the meaning of H'(6) in the context of the problem.

(b) Explain why there must be at least one time t, for 2 < t < 10, such that H'(t) = 2.

(c) Use a trapezoidal sum with the four subintervals indicated by the data in the table to approximate the average height of the tree over the time interval 2 ≤ t ≤ 10.

(d) The height of the tree, in meters, can also be modeled by the function G, given by
G(x) = 100x/(1+x), where x is the diameter of the base of the tree, in meters. When the tree is 50 meters tall, the diameter of the base of the tree is increasing at a rate of 0.03 meter per year. According to this model, what is the rate of change of the height of the tree with respect to time, in meters per year, at the time when the tree is 50 meters tall?

(This was on the no-calculator section of the recently-released AP Calculus AB 2018 exam so I appreciate it if you tried to limit calculator usage)

Answer 1

(a)


`\displaystyle H'(6) \approx (H(7)-H(5))/(7 -5) = (5)/(2)\text{ meters per year}`

____________

(b)

Since function H is differentiable, it is a continuous function. The Mean Value Theorem guarantees that there is a time t in the interval 3<t<5 such that


`\displaystyle H'(t) = (H(5)-H(3))/(5-3) = (6-2)/(2) = 2`

Since 3<t<5 is contained inside 2<t<10, there there must be at least one t in the interval 2<t<10 such that H'(t) = 2.

____________

(c)


`\displaystyle H_(avg) = (1)/(10-2) \int_2^(10) H(t)\, dt`

where


`\int_2^(10) H(t)\, dt \\ \\ \approx (1)/(2)(1.5+2)(3-2) + (1)/(2)(2 + 6)(5-3) \\ \\ \qquad\qquad {} + (1)/(2)(6 + 11)(7-5) + (1)/(2)(11 + 15)(10-7) \\ \\ = (263)/(4)`

thus


`\displaystyle H_(avg) \approx (1)/(8) \left( (263)/(4) \right) = (263)/(32)\text{ meters}`

____________

(d)

When the tree is 50 minutes tall, the tree has a diameter x. This x value is


`\displaystyle 50 = (100x)/((1+x)) \implies 50(1+x) = 100x \implies x = 1`

Since the height is G, then by implicit differentiation


`\displaystyle(dG)/(dt) = \frac{(1+x)(100 \tfrac{dx}{dt}) - 100x \tfrac{dx}{dt}}{(1+x)^2} \\ \\ \left.(dG)/(dt)\right|_(G = 50) = ((1+1)(100 \cdot 0.03) - 100(1)(0.03))/((1+1)^2) \\ \\ = (3)/(4)\text{ meters per year}`

Answer 2

a) Use the mean value theorem.


`H'(6)\approx(H(7)-H(5))/(7-5)=\frac{11-6}2=\frac52\text{ meters/year}`


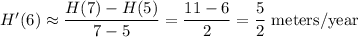
Since
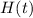
`H(t)` gives the tree's height in meters at time
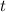
`t`, the value of
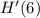
`H'(6)` informs us how quickly the tree is growing exactly after 6 years have passed. (i.e. the instantaneous rate of change of the tree's height)


b) We use the mean value theorem again. Observe that
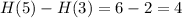
`H(5)-H(3)=6-2=4`, and that
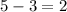
`5-3=2`. By the MVT, there must be some
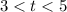
`3<t<5` such that



`H'(t)=\frac42=2`


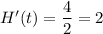
c) The average height of the tree is given by the integral



`\displaystyle\frac1{10-2}\int_2^(10)H(t)\,\mathrm dt`


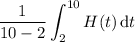
If you can remember the formula for the area of a trapezoid, then this is pretty easy to compute. With five data points, you end up with four trapezoids constructed by the four adjacent subintervals. The "bases" are given by the values of
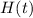
`H(t)` at each pair of endpoints, and the "heights" are the lengths of the subintervals. For the integral itself, we get



`\frac{2+1.5}2(3-2)+\frac{6+2}2(5-3)+\frac{11+6}2(7-5)+\frac{15+11}2(10-7)=\frac{263}4`

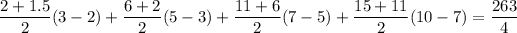
So the average height of the tree (in meters) is



`\displaystyle\frac1{10-2}\int_2^(10)H(t)\,\mathrm dt\approx(263)/(32)`


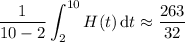
d) When
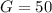
`G=50`, the diameter of the base can be determined to be



`50=(100x)/(1+x)\implies x=1`


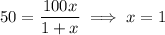
We're told that
`(\mathrm dx)/(\mathrm dt)=0.03`.
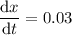
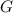
`G` is a function of
`x` which is in turn a function of
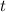
`t`, so when we differentiate, we use the chain rule:



`(\mathrm dG)/(\mathrm dt)=(\mathrm dG)/(\mathrm dx)\cdot(\mathrm dx)/(\mathrm dt)`



`\implies(\mathrm dG)/(\mathrm dt)=(100)/((1+x)^2)\cdot\frac3{100}=\frac3{(1+x)^2}`


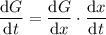
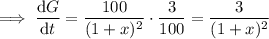
When the height of the tree is 50 meters, we found the diameter to be 1 meter, so at this point



`(\mathrm dG)/(\mathrm dt)=\frac34\text{ meters/year}`