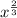Which expression is equivalent to (x^4/3 x^2/3)^1/3?

Question

asked Apr 23, 2019 231k views

2 Answers

Hybrid · Answer 1 · 2019-04-29T11:43:53+0000

Answer : The correct option is,
$x^{(2)/(3)}$

Step-by-step explanation :

The given expression is :

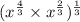
$(x^{(4)/(3)}* x^{(2)/(3)})^{(1)/(3)}$

First we have to solve the term present in the bracket.

Identity used :

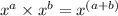
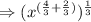
$\Rightarrow (x^{((4)/(3)+(2)/(3))})^{(1)/(3)}$

By the adding the powers of 'x', we get:

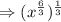
$\Rightarrow (x^{(6)/(3)})^{(1)/(3)}$

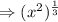
$\Rightarrow (x^(2))^{(1)/(3)}$

Now we have to use identity
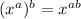, we get :

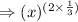
$\Rightarrow (x)^{(2* (1)/(3))}$

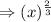
$\Rightarrow (x)^{(2)/(3)}$

Therefore, the correct option is,
$x^{(2)/(3)}$