Question

Write the sum using summation notation, assuming the suggested pattern continues. 16 + 25 + 36 + 49 + ... + n2 + ...

Answer 1

`\bf \stackrel{4^2}{16}+\stackrel{5^2}{25}+\stackrel{6^2}{36}+\stackrel{7^2}{49}+...\qquad \qquad \qquad \sum\limits_(i=4)^(\infty)~i^2`

Answer 2

Hence, the sum using summation notation, assuming the suggested pattern continues
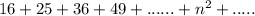`16+25+36+49+......+n^2+.....` is:

`\sum_(n=4)^(\infty)n^2`

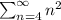
Explanation:

We have to write the sum using summation notation, assuming the suggested pattern continues:

`16+25+36+49+......+n^2+.....`

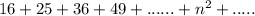
Clearly we may also write this pattern as:

`4^2+5^2+6^2+.....+n^2+......`

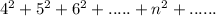
So, in terms of the summand it is written as:

`\sum_(n=4)^(\infty)n^2`

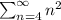
( We have started our summation from 4 since the term in the summation starts with 16 which is 4^2 and goes to infinity )