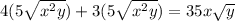Question

What is the following sum? 4(5 sqrt x^2y)+3(5 sqrt x^2y)

Answer 1

7(5 sqrt x^2y) or C

Explanation:

Answer 2

ANSWER



`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} ) = 35x√(y)`


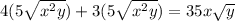
EXPLANATION

The given expression is

`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} )`


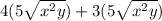
We need to simplify the above expression first before, we add them.


Let us deal with the expressions within the parenthesis first,


`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} ) = 4(5 \sqrt{ {x}^(2)}* √(y) ) + 3(5 \sqrt{ {x}^(2) } * √(y) )`


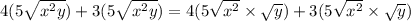
This will simplify to,


`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} ) = 4(5 x* √(y) ) + 3(5 x * √(y) )`


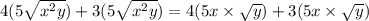
We now multiply out the brackets to obtain,


`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} ) = 20 x* √(y) + 15 x * √(y) )`


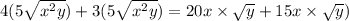
This implies that,


`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} ) = 20 x√(y) + 15 x √(y) )`


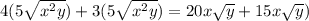
This will give us,


`4(5 \sqrt{ {x}^(2)y } ) + 3(5 \sqrt{ {x}^(2) y} ) = 35x√(y)`