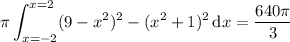Use the washer method. Refer to the attached image below, which shows one such washer used to approximate the volume.
The volume of this kind of washer is
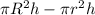
, where
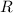
is the radius of the larger cylinder and

is the radius of the smaller cylinder. The height

is the same for both and is given by
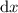
, an infinitesimal change in

. The radius of the larger cylinder is
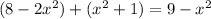
, while the radius of the smaller cylinder is just

.
The two parabolas intersect at

, so the volume of this solid is given by