Question

Two floors in a building are separated by 4.1 m. People move between the two floors on a set of stairs. (a) Determine the change in potential energy of a 3.0 kg backpack carried up the stairs. (b) Determine the change in potential energy of a person with weight 650 N that descends the stairs.

Answer 1

a) The change in potential energy of a 3.0 kilograms backpack carried up the stairs.

b) The change in potential energy of a persona with weight 650 newtons that descends the stairs is -2665 joules.

Step-by-step explanation:

Let consider the bottom of the first floor in a building as the zero reference (
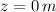`z = 0\,m`). The change in potential energy experimented by a particle (
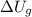`\Delta U_(g)`), measured in joules, is:

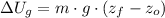`\Delta U_(g) = m\cdot g\cdot (z_(f)-z_(o))` (1)

Where:

`m` - Mass, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

`z_(o)`,
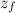`z_(f)` - Initial and final height with respect to zero reference, measured in meters.

Please notice that
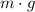`m\cdot g` is the weight of the particle, measured in newtons.

a) If we know that
`m = 3\,kg`,
`g = 9.807\,(m)/(s^(2))`,
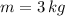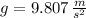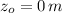`z_(o) = 0\,m` and
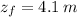`z_(f) = 4.1\,m`, then the change in potential energy is:

`\Delta U_(g) = (3\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (4.1\,m-0\,m)`

`\Delta U_(g) = 120.626\,J`

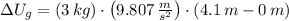
The change in potential energy of a 3.0 kilograms backpack carried up the stairs.

b) If we know that
`m\cdot g = 650\,N`,
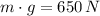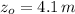`z_(o) = 4.1\,m` and
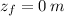`z_(f) = 0\,m`, then the change in potential energy is:

`\Delta U_(g) = (650\,N)\cdot (0\,m-4.1\,m)`

`\Delta U_(g) = -2665\,J`

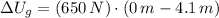
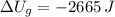
The change in potential energy of a persona with weight 650 newtons that descends the stairs is -2665 joules.