Deposit made each year = $1000
Compound interest = 6%
Time period = 30 years
When a deposit is made each year with interest compounded annually, total amount after a certain time period is given as:
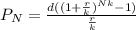
where,
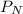 = total amount in account after N years.
= total amount in account after N years.
d = deposit made
r = annual rate of interest in decimal form.
k = number times deposit made in one year.
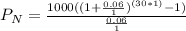
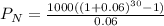
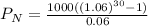
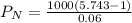
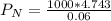
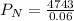
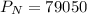
Hence, value in the account at the end of 30th year = $79050