Answer:
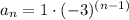
Explanation:
We have been given a geometric sequence and we are asked to find the explicit formula for our given sequence.
The explicit formula of geometric sequence is in form:
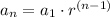 , where,
, where,
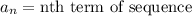 ,
,
 ,
,
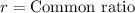 ,
,
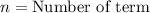 .
.
First of all, let us find common ratio of our given sequence by dividing one term by its previous term.
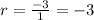
We can see that 1st term of our given sequence is 1. Upon substituting our given values in explicit form of geometric sequence we will get,
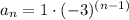
Therefore, the explicit formula for our given sequence is
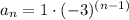 .
.