Answer:
b. 25/32
Explanation:
To evaluate the function
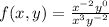
When
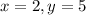 we replace x by 2 and y by 5 in the function. So:
we replace x by 2 and y by 5 in the function. So:
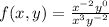
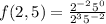
Expressions wth negative exponents in the numerator go to the denominator with positive exponent. On the denominator goes to the numerator with positive exponent. So:
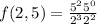
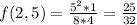
The correct answer is
b. 25/32