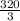Answer:
Hence, the steady state temperature distribution between concentric spheres with radii 1 and 4 is:
u =
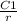 + C2
+ C2
u =
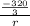 +
+
Step-by-step explanation:
Solution:
Note: This question is incomplete and lacks necessary data to solve this question. But I have found a similar question and will try to solve it.
This question has this following part missing:
"If the temperature of the outer sphere is maintained at 80 degrees and the inner sphere at 0 degrees.
Now, this question is complete.
Let's find out the steady state temperature distribution.
As, we know the spherical symmetric heat equation:
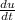 =
=
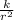
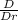 (
(
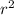
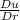 )
)
Where, small (d) represents the partial differentiation and Capital D represents simple derivative.
And the ordinary differential equation (ODE) for steady state temperature distribution is:
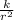
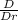 (
(
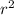
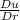 ) = 0
) = 0
So it can be said that:
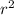
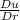
Consequently,
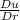 =
=
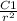
Taking derivative of the above equation we get:
u = -
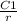 + C2
+ C2
Solution of the ordinary differential equation
u =
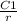 + C2 (Consuming the negative sign into C1 constant)
+ C2 (Consuming the negative sign into C1 constant)
As, it is given in our question that our boundary conditions are: 1 and 4
So,
Putting the boundary conditions into the variable (r) to find the constants we get:
u1 =
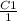 + C2 = 0 (degrees)
+ C2 = 0 (degrees)
u1 = C1 + C2 = 0 (degrees) equation (1)
Similarly,
u4 =
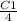 + C2 = 80 (degrees)
+ C2 = 80 (degrees)
u4 =
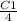 + C2 = 80 (degrees) equation (2)
+ C2 = 80 (degrees) equation (2)
Solving for C1, we get:
Equation 1 - Equation 2
(C1 - C2 = 0) - (
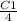 + C2 = 80)
+ C2 = 80)
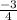 C1 = 80
C1 = 80
Solving for C1
C1 = -
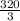
With the help of value of C1, we get value of C2
Put the value of C1 in equation (1) to get value of C2
C1 + C2 = 0
-
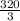 + C2 = 0
+ C2 = 0
Solving for C2
C2 =
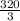
Hence, the steady state temperature distribution between concentric spheres with radii 1 and 4 is:
u =
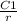 + C2
+ C2
Plugging in the values of C1 and C2
u =
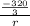 +
+